Оглавление

1. Начало
2. Элементарная ячейка памяти
3. Регистр
4. Декодер и оперативная память
5. Арифметико-логическое устройство

2. Элементарная ячейка памяти

Понятие памяти

Итак, что такое память и в каком смысле можно сказать, что предметы могут обладать памятью? Для ответа на этот вопрос, давайте проведем эксперимент: ударим бетонную стену. Ну или можно не бить, а просто это представить :) А теперь посмотрим на эту стену: запечалился ли на ней наш удар? Скорее всего – нет. То есть глядя на стену нельзя сказать: били ее мы или нет.

В этом смысле можно утверждать, что стена “ничего не запомнила”, поскольку наше на нее воздействие на ней самой никак не отразилось. Теперь же ударим по  картонной коробке. А вот в данном случае мы уже увидим, что коробка деформировалась и что, в отличии от стены она имеет “память на удар”. Это достаточно простое сравнение поможет прояснить в каком смысле мы можем употреблять слово “память” по отношению к предметам: способность изменяться под неким воздействием и сохранять это изменение даже когда воздействие прекратилось. Теперь вернемся к логическим гейтам.

Самоссылание

Гейты, о которых мы до сих пор говорили не обладают памятью: их выходной сигнал целиком зависит от входного и после изменения последнего тоже меняется, не зависимо от текущего состояния. Но тогда возможно ли вообще сделать логическую схему со способностью хранить сигнал, используя базовые логические элементы? Да, и сейчас мы узнаем как. Давайте соединим два NAND-гейта таким образом: 

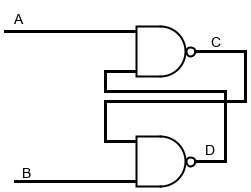
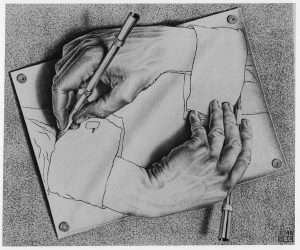
Сходу эта схема может показаться необычной: дело в том что она ссылается сама на себя. Это феномен в виде визуальной метафоры так же можно наблюдать в известной картине Маурица Эшера “Рисующие Руки”.

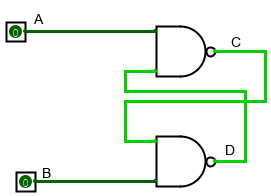
Итак, если на входах A и B у нас нули, то верхний и нижний гейты будут выдавать единицы (поскольку NAND-гейт выдает ноль только когда на обоих его входах единицы).

На этой картинке и в дальнейшем ярко-зеленый цвет провода (носителя сигнала) означает единицу, а темно-зеленый – ноль.

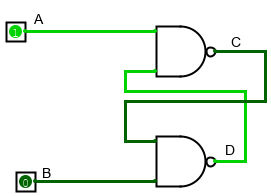
Теперь подадим сигнал 1 на вход A, а на входе B оставим 0: верхний гейт теперь будет выдавать 0, а нижний продолжит выдавать 1.

Теперь, наоборот, подадим сигнал 1 на вход B, а на A пусть будет 0. Картина также изменится на обратную: на выходе верхнего гейта 0, а на выходе нижнего – 1.

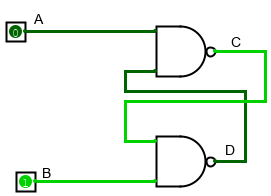
Хорошо, а что будет если на оба входа подать единицы? А вот в таком случае мы получаем необычный результат:  схема сохраняет свое предыдущее состояние.

То есть состояние схемы, когда на обоих ее входах единицы может быть двояким, и зависит от прошлых входных значений. Вот тут мы и натыкаемся на нужное нам свойство схемы: ее поведение зависит не только от входных данных, но и от ее текущего состояния. Давайте используем эту особенность для создания запоминающего устройства.

Запоминающее устройство

Будем использовать выход C для хранении значения. Схема может хранить либо 0 либо 1

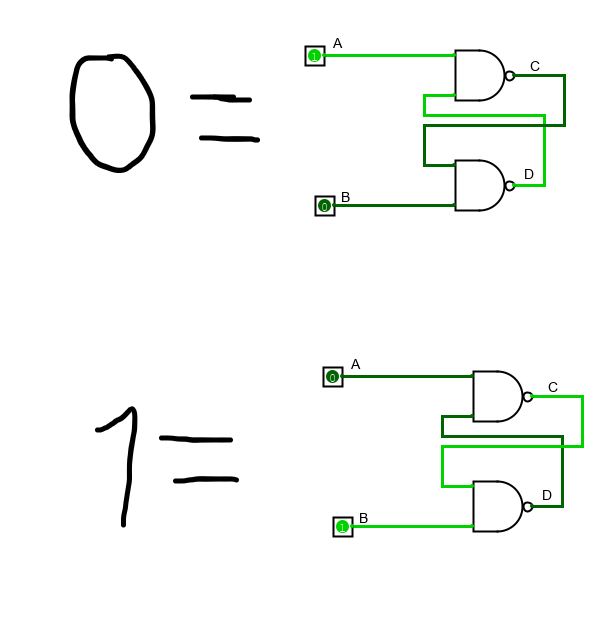
Что бы записать ноль: на A подаем 1, а на B – 0. Что бы записать единицу - делаем все наоборот: на A подаем 0, а на B – 1. После записи нужного нам значения можно подать на оба входа единицы – и значение не изменится. Это значит, что схема “запомнила” нужный нам сигнал. Для автоматизации этого процесса дополним схему еще двумя NAND-гейтами. Точка в месте пересечения двух проводов означает, что сигнал в этом месте раздваивается.

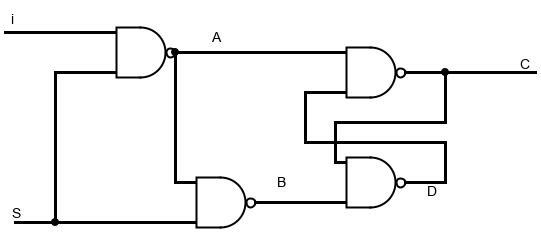
В этой схеме у нас также два входа и один выход. Если S = 0, то I никак не влияет на выходное значение: первый верхний гейт имеет на нижем входе единицу, значит независимо от значения входа I он будет продолжать выдавать единицу

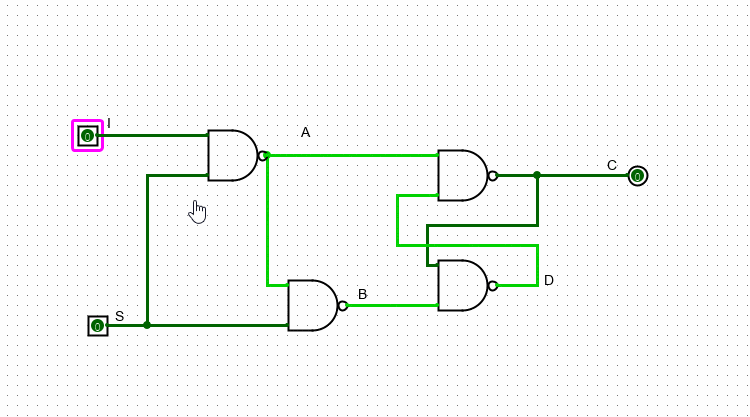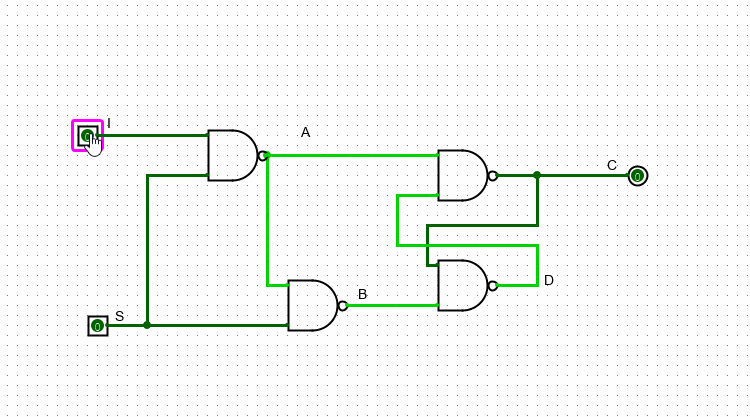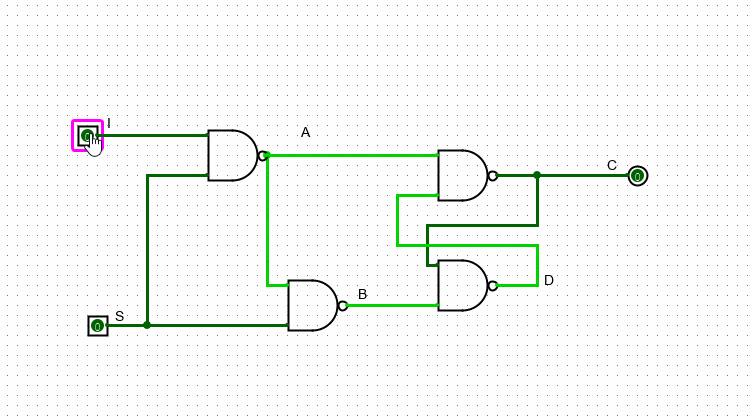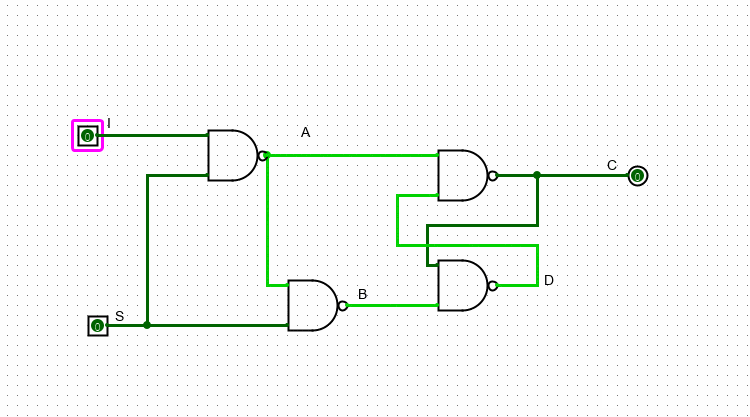
Если же S равно 1, то значение I уже может влиять на значение выхода. В случае, когда I = 0, A будет равно единице, а B – нулю. Как мы разобрались выше, в данном варианте С будет равно нулю, а D – единице. В случае когда I = 1, наоборот – A будет равно нулю, а B – единице. Следовательно, C=1 и D=0.

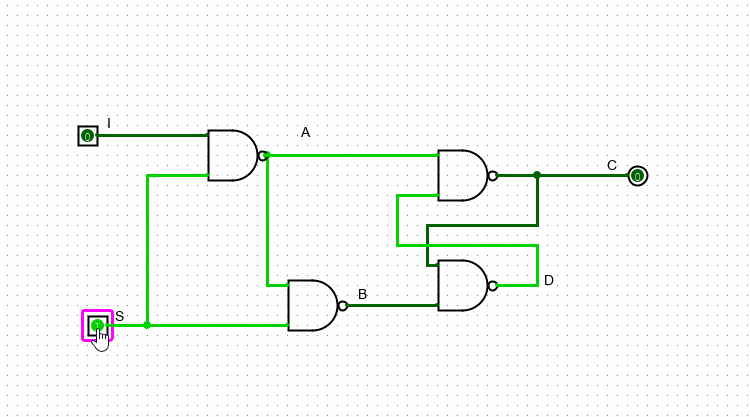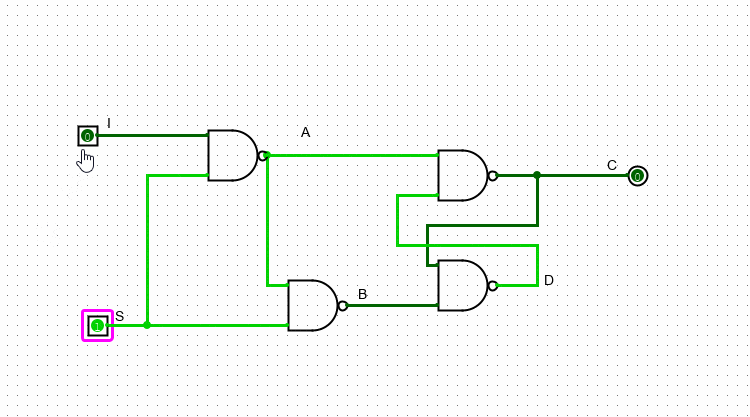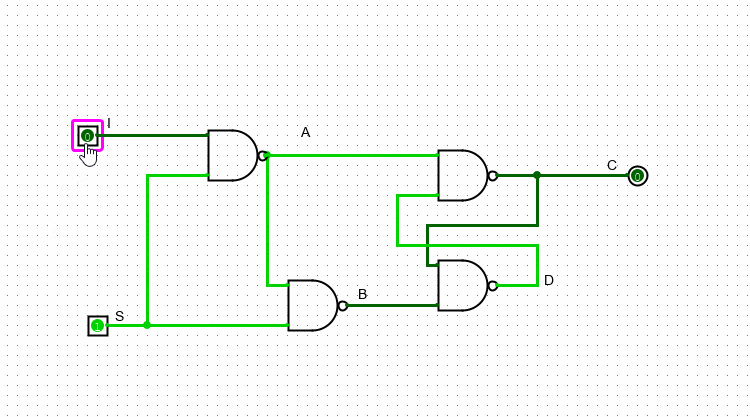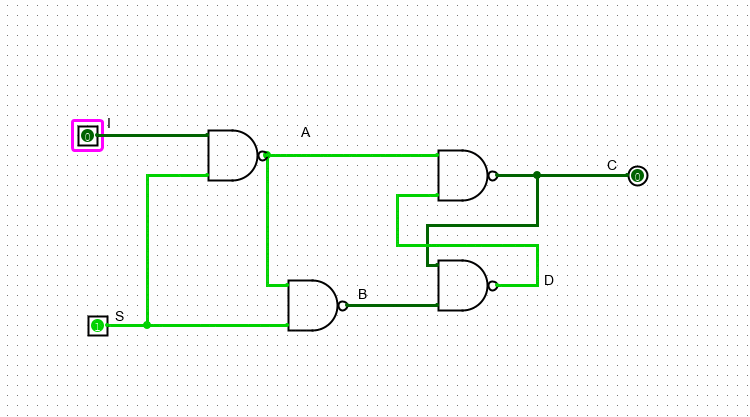
Важно заметить, что значение, которое подается на S выступает неким “разрешением на запись”. Если S = 1, то выходное значение схемы (то значение, которое на хранит) будет совпадать с I. Если же S = 0, то  схема закрыта для изменений и хранит в себе то значение I, которое хранила на момент, когда S была равна единице.

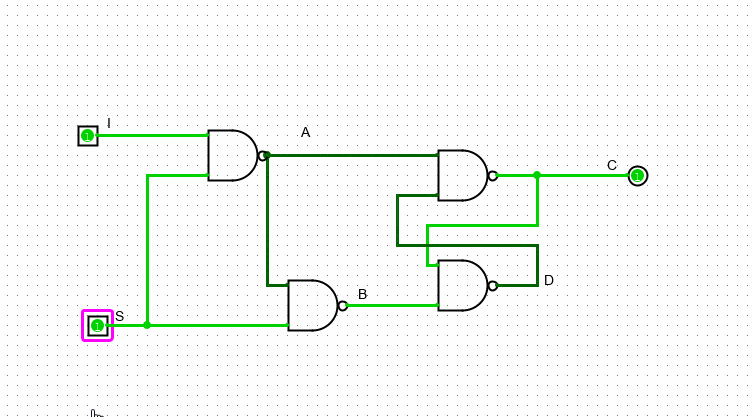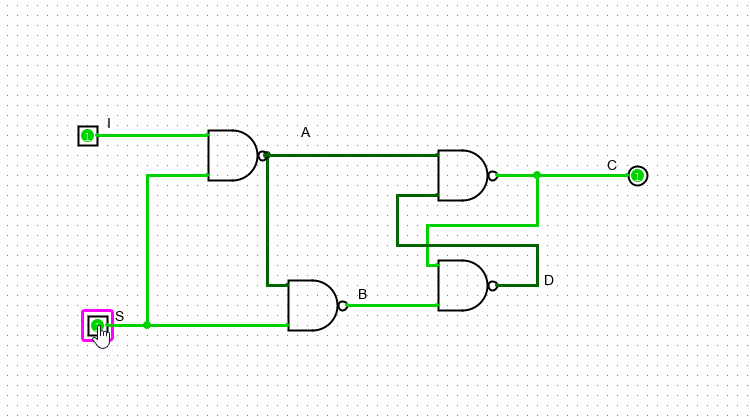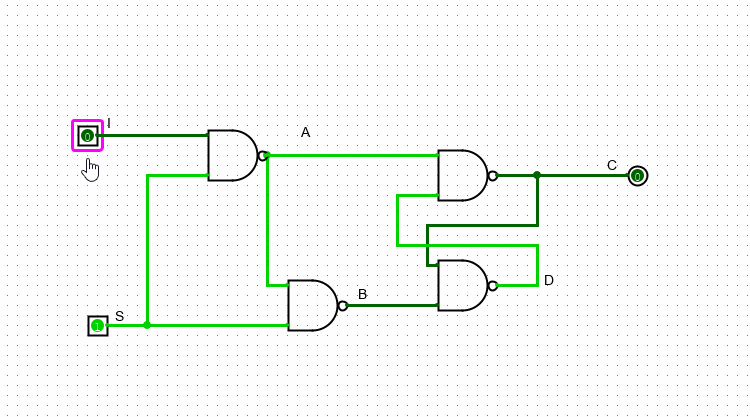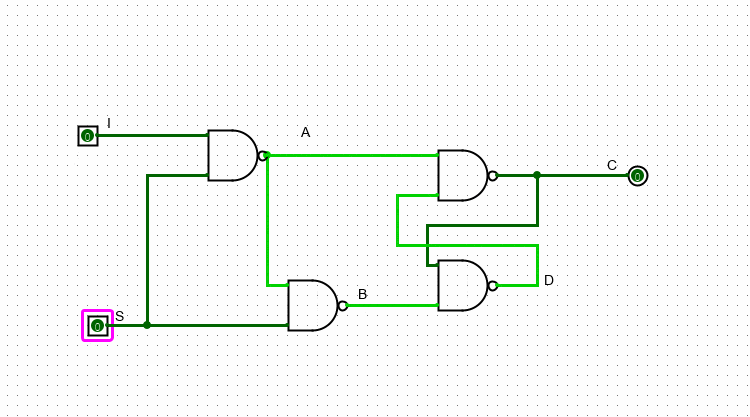
Ячейка памяти

Итак, на основе этой схемы мы можем построить запоминающий элемент. Я изменю имя выхода схемы с С на O (Output – в переводе с английского “выход”. I означает Input – Вход, а S - Set – Установить ). И мы получим такую штуку:

Мы передаем на S единицу, что бы открыть запись, а на I передаем то значение, которое хотим записать (ноль или единицу). Теперь даже после того, как мы закроем возможность для записи это значение будет продолжать там храниться. 

Источники

1. Чарльз Петцольд “Код – тайный язык информатики”;
2. J Clark Scott “But How Do IT Know”;
3. Logisim – программа для симуляции логических схем.