Оглавление

1. Начало
2. Элементарная ячейка памяти
3. Регистр
4. Декодер и оперативная память
5. Арифметико-логическое устройство

5. Арифметико-логическое устройство

Работаем с байтами

Отдельные логические гейты работают с битами, но при проектировании схемы удобнее оперировать целыми байтами. Давайте построим несколько схем, которые будут иметь на входе не бит, а один либо два байта, производить над ними некоторые операции и возвращать также байт. Поскольку компьютер оперирует двумя типами сигнала, нам пригодится знание двоичной системы счисления. Не хочу повторяться, т.к. в интернете есть уже кучу статей и видео на этот счет (например www.youtube.com/watch?v=npB8lF-V4mc). Так что предварительно ознакомьтесь с этой темой, а потом переходите к статье.

Шифтер

Шифтер (от английского shift – сдвиг) представляет собой схему, которая может менять позицию битов в байте, “сдвигая” их значения вправо или влево. Сначала рассмотрим правый шифтер.

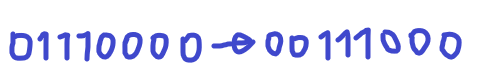
Как видно, мы берем первый байт и ставим его на место второго, второй ставим на место третьего и т.д. Схема правого шифтера выглядит так:

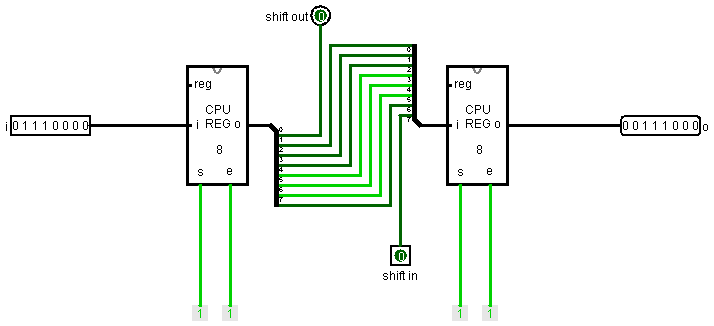
Ничего сложного. У нас есть два регистра, первый – входной, который хранит некий байт, второй - выходной, значение которого является сдвинутым значением первого. Первый бит выходного байта мы задаем произвольно и подаем на вход shift in. Поскольку последнее значение бита во входном регистре как бы теряется, мы делаем для него отдельный выход shift out и передаем его туда.

Теперь рассмотрим как действует левый шифтер.

В отличии от правого шифтера, он сдвигает значения битов, как следует  из названия, влево. Второй бит мы ставим на место первого, третий на место второго и т. д. Его схема:

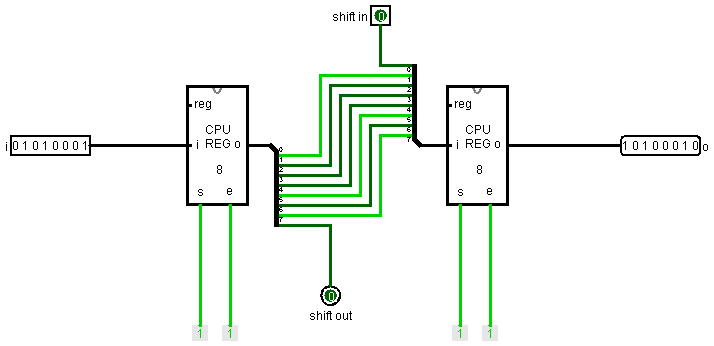
Первый бит входного регистра мы передаем на выход shift out. Последний бит выходного регистра берется из входа shift in.

Теперь изобразим шифтеры в виде блоков.

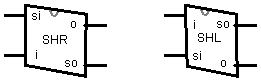
NOTer

Noter (от английского NOT – нет) представляет собой простую схему. На вход мы подаем байт, а выходе получаем “отрицание” этого байта:

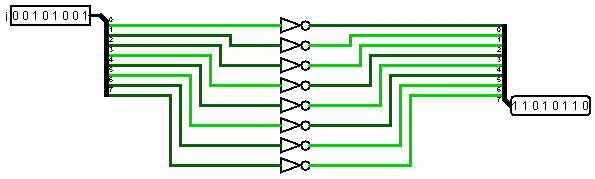
Изобразим его также в виде единого блока:

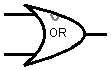
ORer

Orer (от английского OR – или) имеет на входе два байта, производит операцию OR между ними и передает результат на выход.

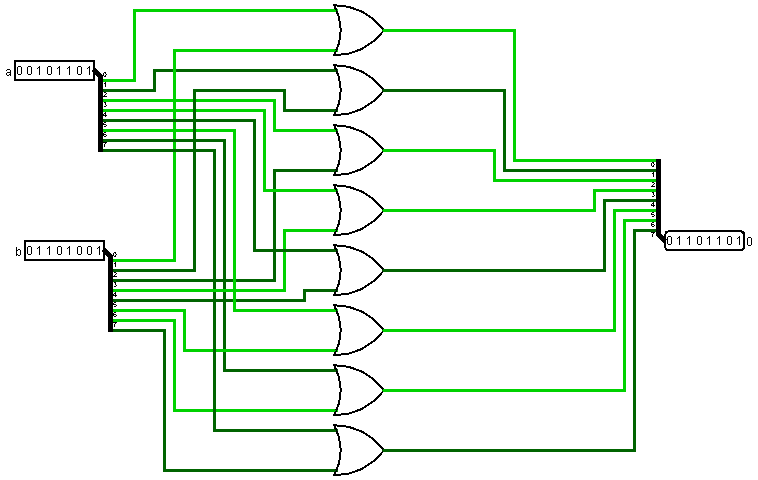
В виде единого блока:

Adder

Adder (от английского add – добавить) получает на входе два байта, складывает их и результат передает на выход. Сначала посмотрим как можно сложить два двоичных числа, например 101 и 111, в столбик. Сначала складываем две последних цифры. 1 + 1 = 10. Ноль пишем, единицу переносим. Потом складываем следующие цифры после последних 1+0=1. Единицу мы переносили прибавляем также ее 1+1 = 10, опять пишем ноль, переносим единицу. Складываем последние цифры 1+1 = 10. Единицу мы переносили: 10+1 =11. В итоге результат 1100.

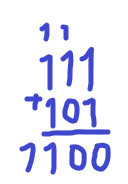
Теперь попробуем реализовать этот принцип на схеме. Начнем с того, что бы просто сложить два бита. Варианты могут быть следующие:

В первых трех случаях мы просто пишем итоговое число, в последнем мы пишем 0, а единицу переносим. Логическая схема, с таким функционалом выглядит так:

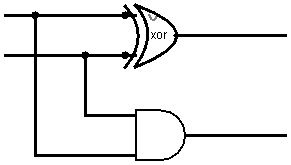
Итак, у схемы два входа и два выхода. На вход подаются два бита, которые мы складываем. На верхнем выходе то значение, что мы пишем, а на нижнем – то, что переносим.

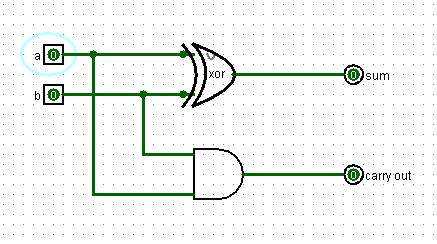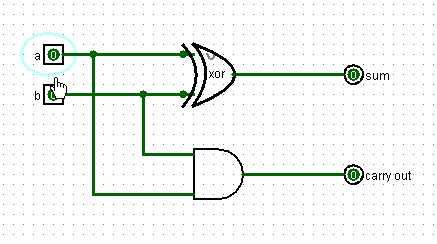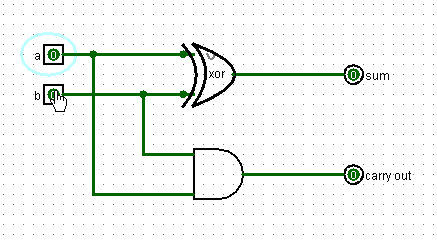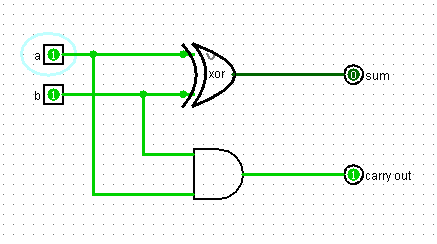
Но в реальном сложении, как мы помним, помимо того, что бы сложить, два бита необходимо учитывать третий бит: результат переноса от предыдущего сложения. Если он равен единице его также необходимо прибавить к сумме. Поэтому улучшим схему таким образом:

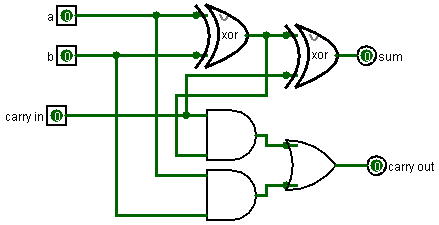
Мы складываем два бита и к их сумме еще прибавляем значение предыдущего переноса.

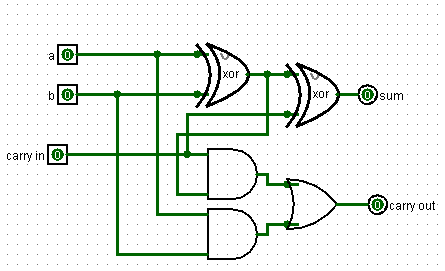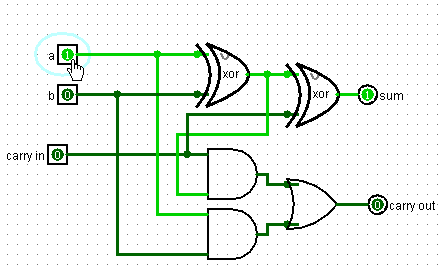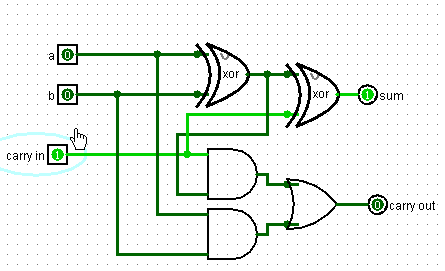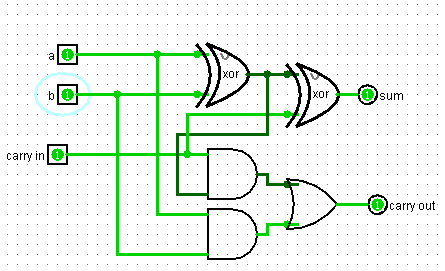
Итак, у нас есть Adder, способный складывать два бита.

Построим теперь Adder, который будет складывать целый байт:

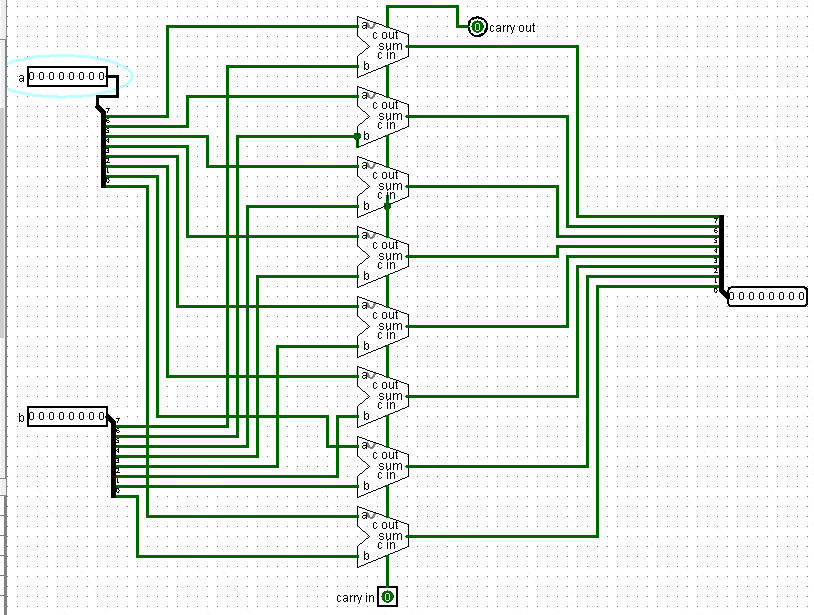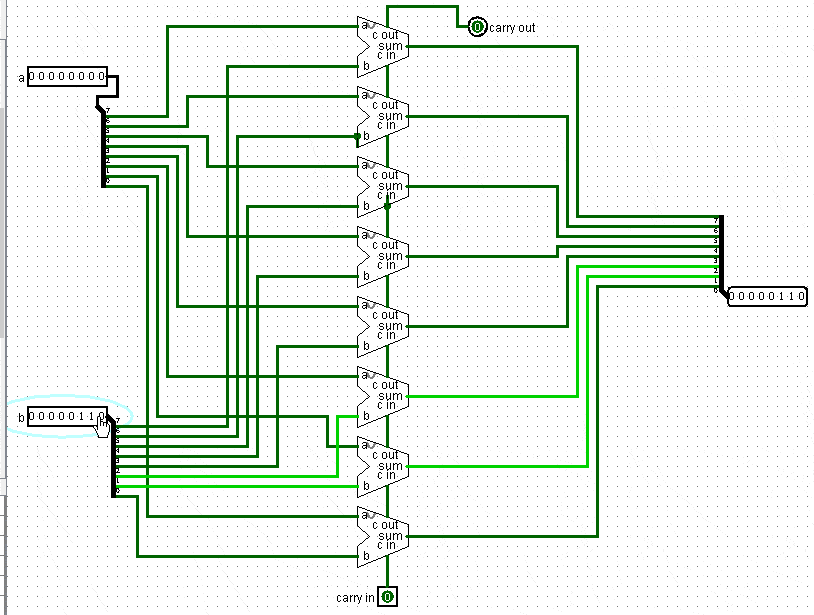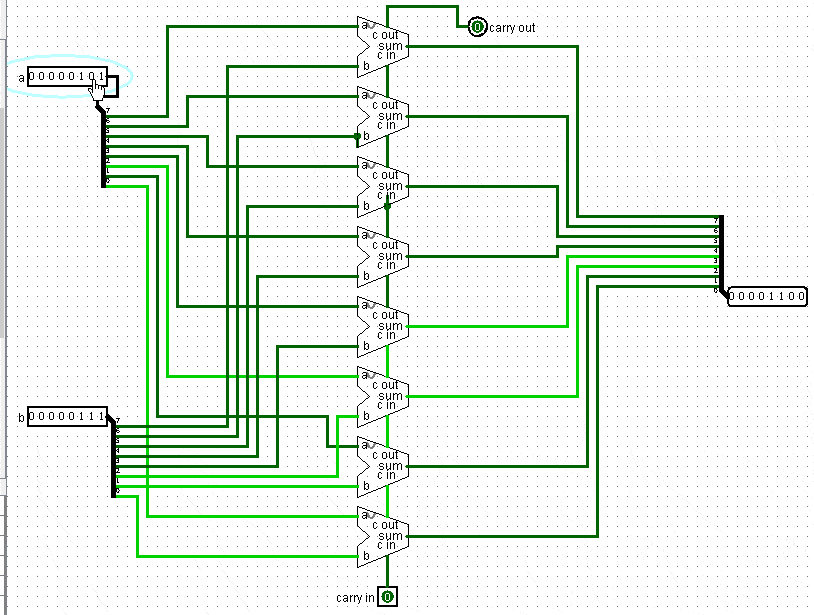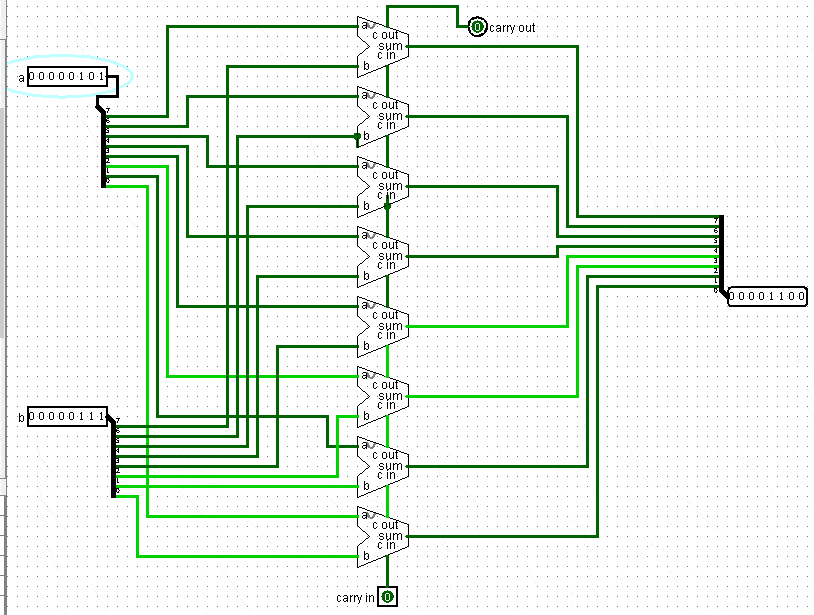
Мы принимаем два байта выход и складываем две каждые цифры соответствующих разрядов, результат выдаем на вход.

Изобразим Adder в виде единого блока.

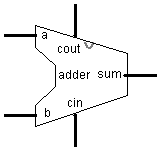
Сравнитель

Теперь построим схему, которая получает на входе два байта, сравнивает их и определяет равны ли они между собой, либо первый байт больше второго. Помимо этого эта схема будет делать операцию XOR между этими байтами и отправлять результат на выход. Два одном, так сказать.

Как мы сравниваем двоичные числа? Сначала сравниваем первые цифры, если какая-то цифра больше, то и само это число больше.

Если же эти цифры равны, то сравниваем вторые числа, если какое-то из них больше, то и само число, содержащее эту цифру больше. Если они снова равны – то переходим к третьим по-счету цифрам и т.д. В итоге окажется, что либо какое-то число, либо числа равны. Построим логическую схему, которая выполняет подобный алгоритм. Рассмотрим элемент схемы, сравнивающий значения двух текущих битов.

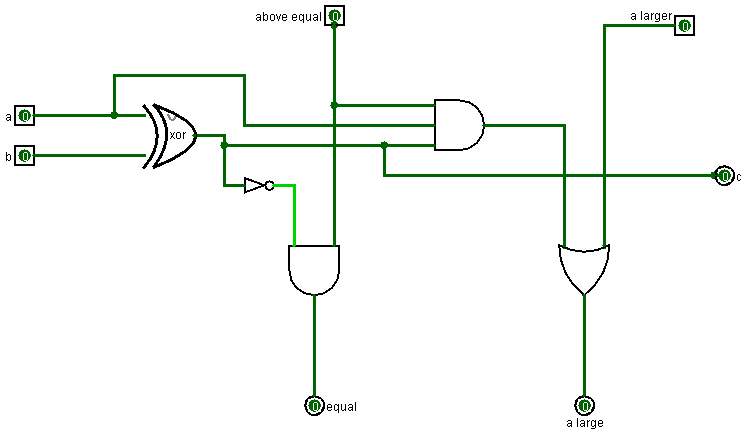
На выход a и b подаются текущие значение битов двух чисел, которые мы сравниваем.

Логика сравнения основано на принципе, описанном выше. Операция сравнения двух текущих битов некого числа зависит от результатов сравнения двух предыдущих битов.  Если значение предыдущего бита числа a было больше чем значение предыдущего бита числа b, то на вход a lager подается единица, а на вход above equal – ноль. Это означает, что число a больше числа b, значит на выходе схема при любых текущих значениях битов чисел a и b выдает единицу на выход a lager. На выход c схема всегда выдает результат операции a XOR b, это ее дополнительная функция помимо сравнения.

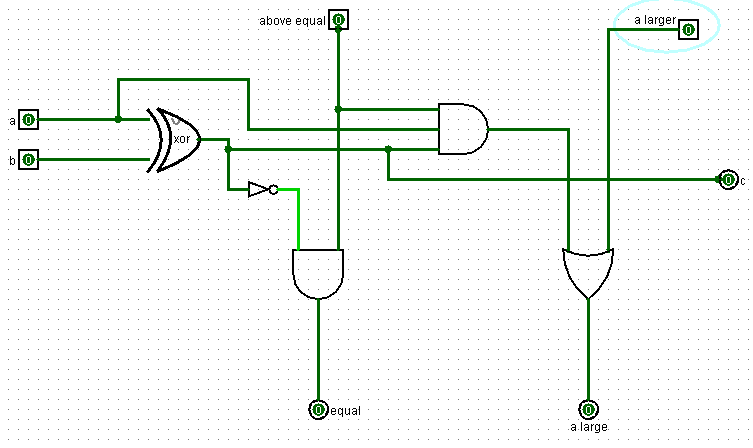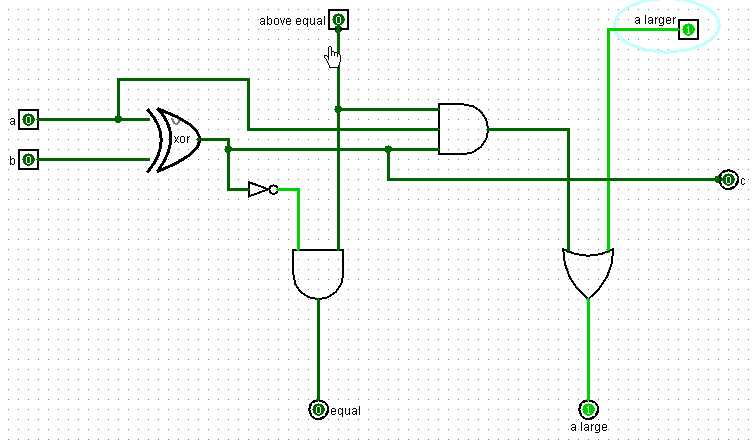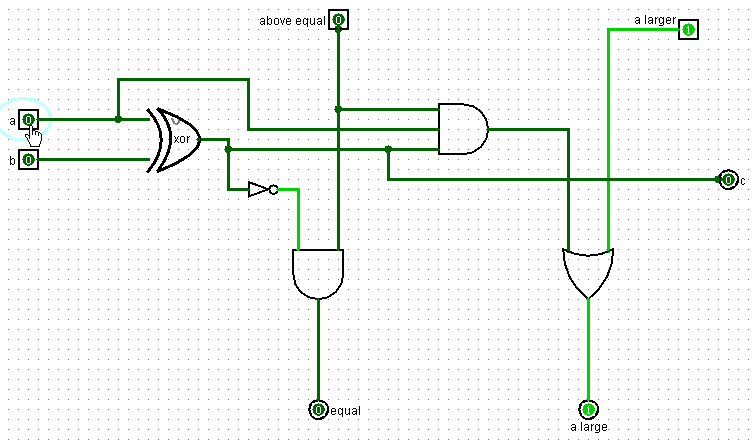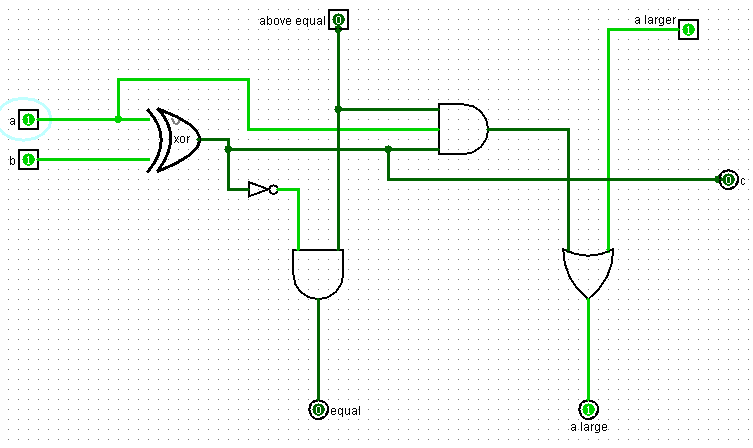
Если предыдущее значение бита a меньше чем предыдущее значение бита b, то и само число a меньше числа b. Тогда схема имеет нули на входах above equal и a larger. И, соответственно, выдает нули на выходы equal и a larger.

Если предыдущие значения битов чисел a и b равны, то схема получает единицу на вход above equal, и ноль на вход a lager. В таком случае схема сравнивает текущие значения битов a и b. И, если они равны, выдает единицу на выход equal и ноль на выход a lager, если бит a больше бита, b выдает единицу на выход a lager и ноль на выход equal, а если биты a и b равны выдает нули на оба этих выхода.

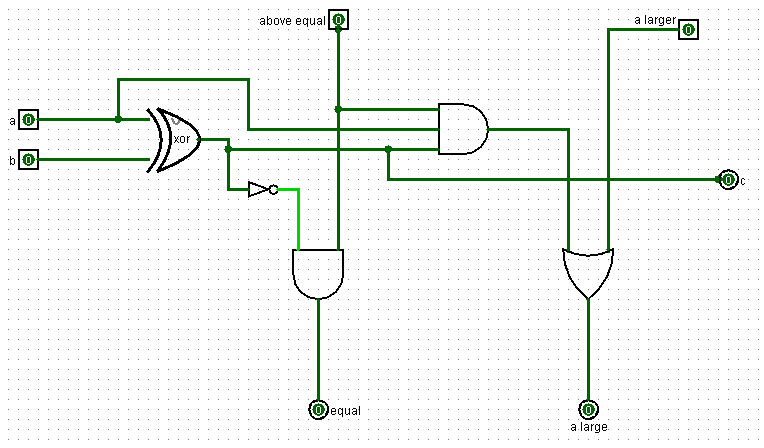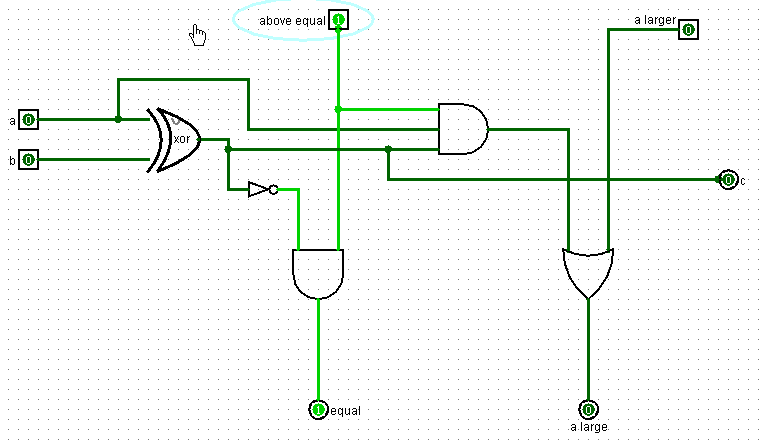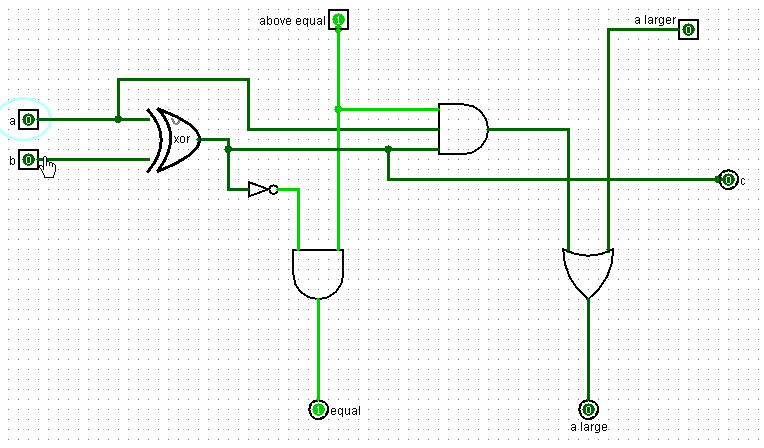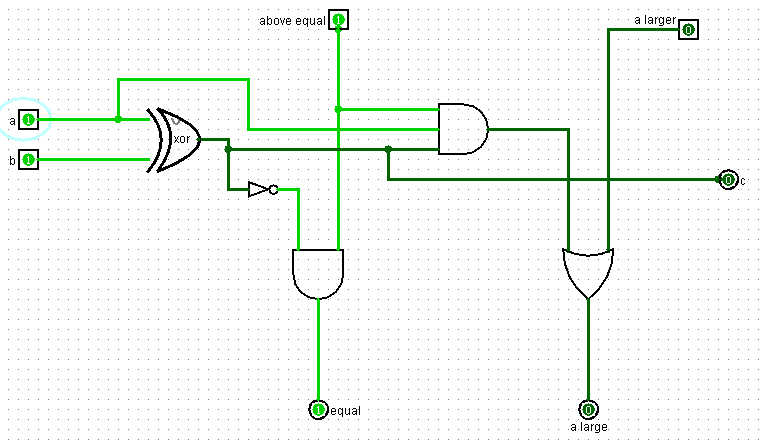
Эта схема, сравнивающая отдельные биты (битовый сравнитель) в виде единого блока выглядит так:

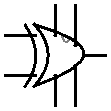
Теперь рассмотрим устройство сравнителя, который может сравнивать два байта друг с другом:

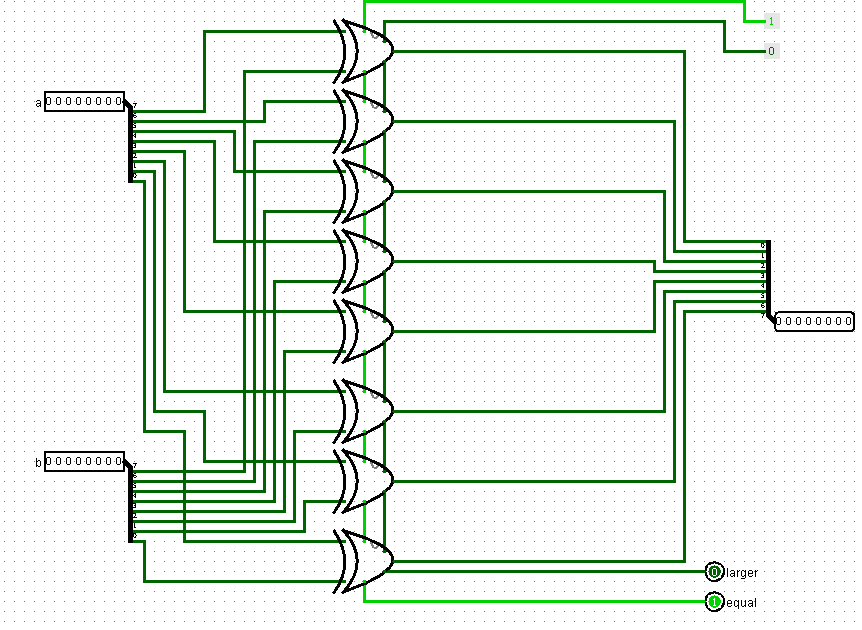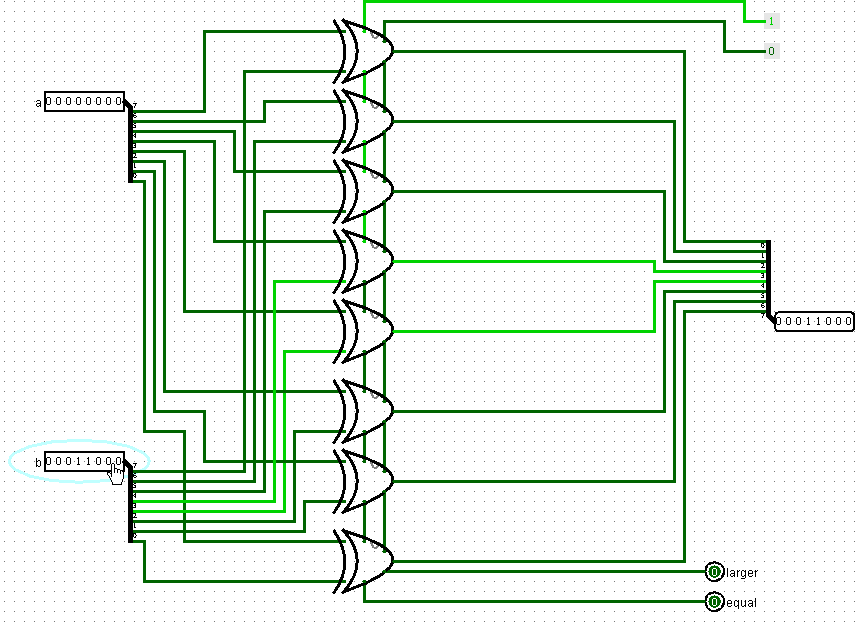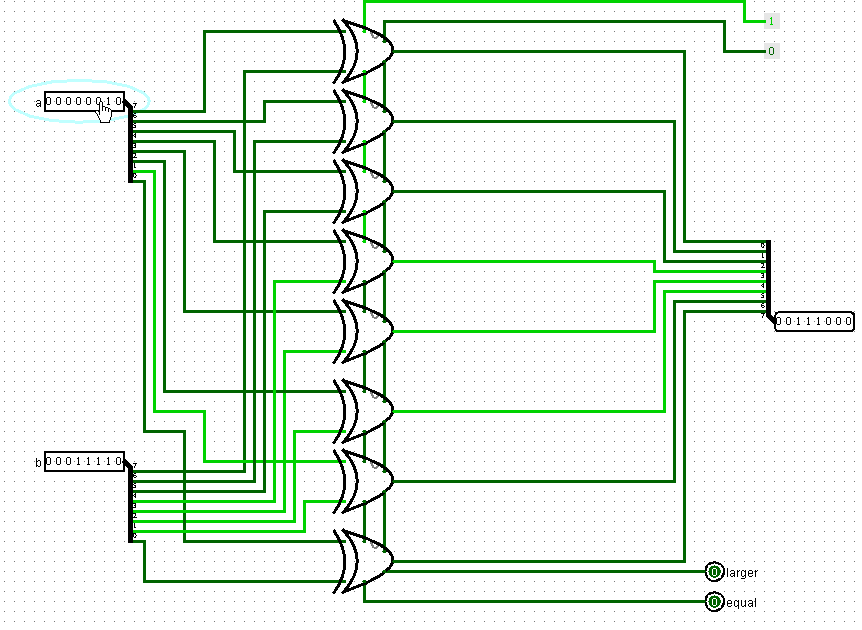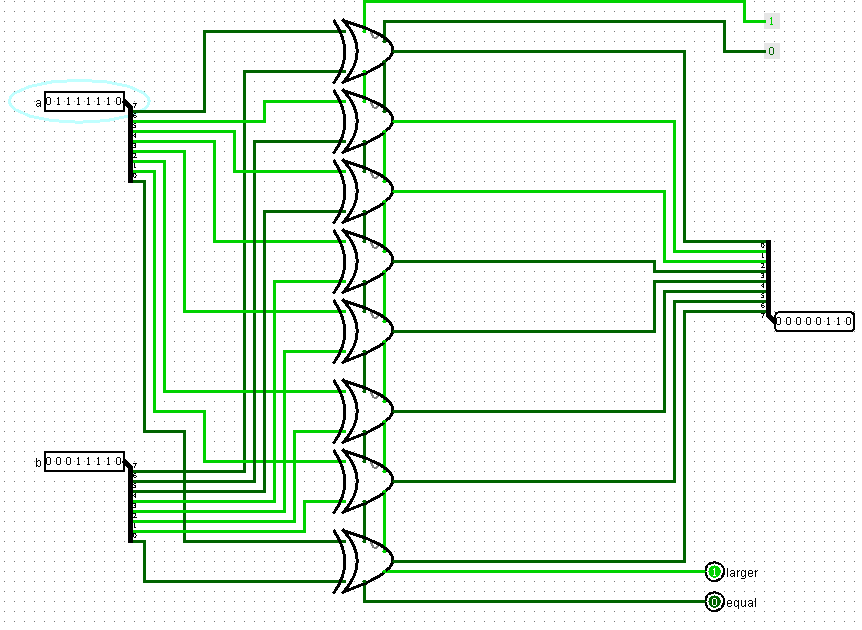
Как видно, схема содержит в себе восемь битовых сравнителей.

На входы мы подаем байты a и b. Мы сравниваем каждый бит соответствующих разрядов этих байтов. Если они равны, то на выходе equal единица, а на выходе lager 0. Если a больше b, то - наоборот. Если b больше a, то на обоих этих выходах нули. Помимо сравнения эта схема также ксорит (делает операцию XOR) два входящих байта и выдает получившийся третий байт.

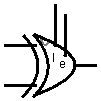
Байтовый сравнитель в виде единого блока выглядит так:

Арифметико-логическое устройство целиком

Теперь объединим все упомянутые выше схемы в рамках одного устройства:

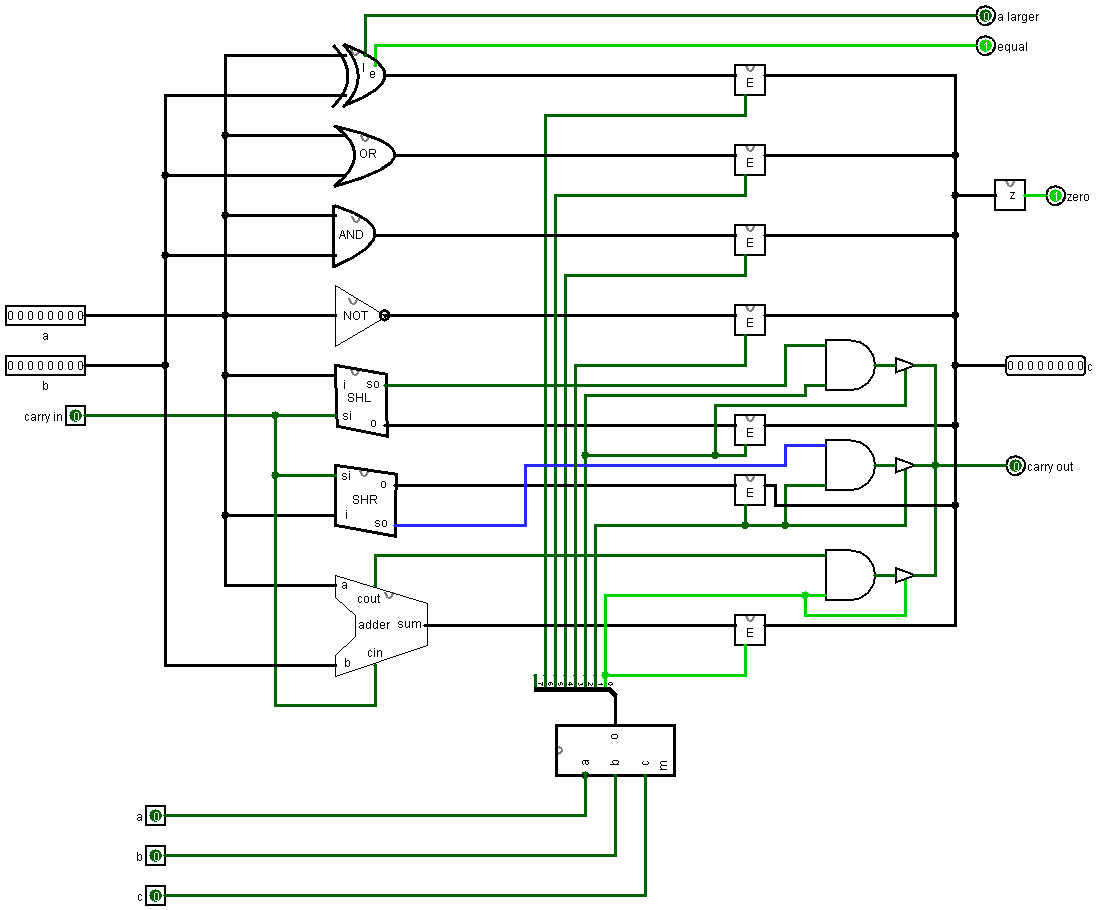
Блоки E это энейблеры, которые пропускают либо блокирует входящий сигнал. В зависимости от значений нижних входов (один –  пропустить, ноль – блокировать).

Смысл такой, что мы имеет два байта, над которыми хотим сделать какие-либо операции. Значения этих байтов передается в блоки, которые мы описали выше (шифтер, adder  и т.д.) Блоки выполняют необходимые операции, но информация  с результатами всех этих операций останавливается на энейблерах. В самом низу мы видим декодер, с помощью которого мы можем выбрать, какой энейблер мы хотим активировать. То есть мы можем выбрать какая именно операция из возможных нас интересует и пропустить ее результаты на выход. Что бы лучше в это вкинуть, откройте в Logisim’е эту схему и посмотрите на нее на практике.

Источники

• John Clark Scott “But How Do It Know?”
• Logisim – программа для симуляции логических схем (www.cburch.com/logisim/)
• ScottCPU – название модели компьютера, который мы проектируем, скачать его схему для Logisim’а можно тут