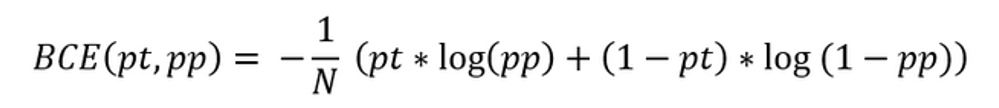Применение нейронной сети на основе архитектуры U-NET с целью детектирования искомых объектов на изображениях на примере детектирования активных элементов на фотографиях печатных плат

Оглавление:

• Введение

• Описание архитектуры U-net класса сверточных нейронных сетей

• Реализация модели нейронной сети на основе архитектуры U-net класса сверточных нейронных сетей

• Экспериментальное обоснование полезности обученной модели нейронной сети на основе архитектуры нейронной сети U-net путем анализа числовых характеристик допущенных ошибок при детектировании

• Направление дальнейших исследований

ПРИМЕНЕНИЕ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ АРХИТЕКТУРЫ U-NET С ЦЕЛЬЮ ДЕТЕКТИРОВАНИЯ ИСКОМЫХ ОБЪЕКТОВ НА ИЗОБРАЖЕНЯХ НА ПРИМЕРЕ ДЕТЕКТИРОВАНИЯ АКТИВНЫХ ЭЛЕМЕНТОВ НА ФОТОГРАФИЯХ ПЕЧАТНЫХ ПЛАТ

АННОТАЦИЯ. В данной статье проведено исследование эффективности применения нейронной сети на основе архитектуры U-net с целью оптимизации процесса поиска искомых элементов на фотографиях на примере автоматизации поиска активных элементов на фотографиях печатных плат. Предложены методика определения ошибки на выходе сети – применение функции бинарной кросс-энтропии, метод обратного распространения ошибки с целью корректировки весов ядер свертки на этапах понижающей и повышающей дискретизации, оптимальный оптимизатор Адам для поиска минимального значения функции ошибки.

КЛЮЧЕВЫЕ СЛОВА: сверточная нейронная сеть, архитектура U-net, сегментация, оптимизация процессов, печатная плата, детектирование.

ВВЕДЕНИЕ

За последние десятилетия необходимость в оптимизации и автоматизации многих немаловажных для человечества процессов возросла в несколько раз, в связи с увеличением производства, тем самым увеличением физического монотонного труда. Одним из оптимальных решений является применение алгоритмов нейронных сетей. Основным преимуществом данного метода является точность и скорость решения поставленной задачи, а также малая вычислительная сложность алгоритма. В данной статье предлагается один из методов оптимизации процесса поиска искомых элементов на фотографиях с высокой точностью, благодаря использованию сверточной нейронной сети на основе архитектуры U-net. Архитектура U-net хорошо зарекомендовала себя на международных соревнованиях по применению алгоритмов нейронных сетей – Kaggle. В дальнейшем, ее областью применения оказалось медицинское программное обеспечение, благодаря своей точности детектирования. Данная архитектура представляет собой двухэтапный процесс анализа обрабатываемого объекта, в частности изображения. Первый этап представляет собой процесс понижающей дискретизации, а второй - повышающей дискретизации. В качестве инструментов моделирования архитектуры U-net в роли обученной модели нейронной сети применяются открытые библиотеки OpenCV и Keras совместно с TensorFlow на базе языка программирования Python.

ОПИСАНИЕ АРХИТЕКТУРЫ U-NET КЛАССА СВЕРТОЧНЫХ НЕЙРОННЫХ СЕТЕЙ

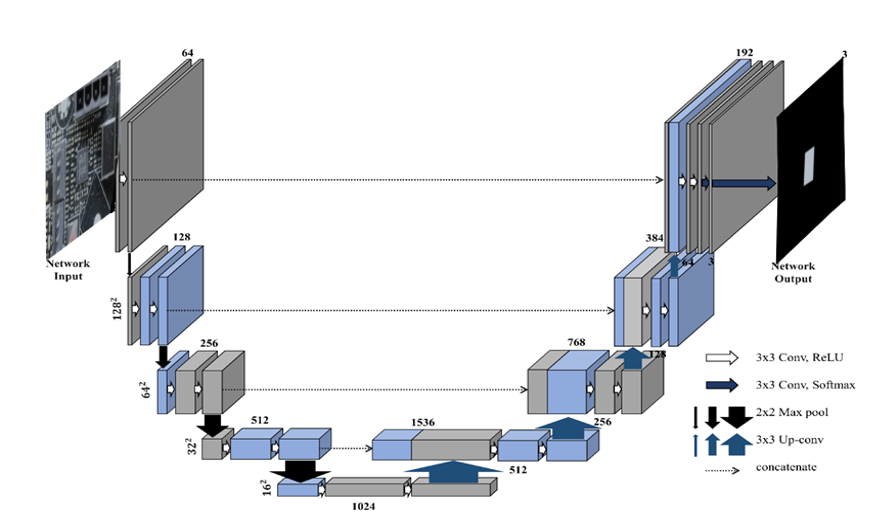
         Схема архитектуры U-net представлена на рис. 1. Данная архитектура относится к классу сверточных нейронных сетей из-за своей структуры и применяемых в ней методов. В классической нейронной сети, называемой полносвязной или регрессивной, имеются входной, выходной и скрытые слои, которые представляют собой набор нейронов, связанных друг с другом. В свою очередь, архитектура U-net не содержит полносвязных слоев, а имеет только карты признаков между входным и выходным слоями, а также ядра свертки для получения и укрепления признаков искомых объектов.

         Первый этап – этап понижающей дискретизации. На данном этапе архитектура U-net получает на вход трехканальное изображение фиксированного размера, которое является степенью двойки по ширине и высоте, с целью сохранения каждого пиксела при применении к изображению или картам признаков метода понижающей дискретизации (downsampling, иначе pooling). На данном этапе формируются ядра свертки, заполняясь случайными значениями, из указанного нами диапазона, чаще всего данный диапазон, представляет собой диапазон [-10; 10]. Над поступившим изображением применяется последовательно методы двух сверток и понижающей дискретизации. Смысл первого этапа заключается в формировании карт признаков искомых объектов, собранных на разных уровнях сворачивания, благодаря чему, данная архитектура способна собирать признаки искомых объектов на изображении, представляющие собой совокупность различных геометрических форм, цветов и размеров, а также других отличительных признаков.

         На втором этапе, этапе повышающей дискретизации, происходит восстановление собранных на первом этапе признаков искомых объектов на изображении. Применяя последовательно метод транспонированной свертки и конкантенации карт признаков с первого этапа на соответствующем уровне 2 этапа, а точнее, последовательное применение методов повышающей дискретизации (upsampling) и свертки, а также конкантенация карт признаков с первого этапа на соответствующем уровне 2 этапа, благодаря чему, происходит сбор восстановленных особенностей искомых объектов на изображении, после применения к ним во втором этапе метода транспонированной свертки, а также особенностей искомых объектов на изображении с первого этапа. Конкантенация карт признаков второго этапа с картами признаков с первого этапа производится с целью сохранения более высокоуровневых особенностей искомых объектов на изображении.

         После сегментации изображения данной архитектурой, на выходе образуется одноканальное бинарное изображение, которое сравнивается с поданной соответствующей сегментируемому изображению маской. Сравнение происходит с целью определения ошибки, допускаемой моделью, в ходе сегментации поданного на вход модели изображения. Определение ошибки производится на основе вычисленного значения несовпадения одноканальных изображений, таких как предсказание модели и соответствующая данному предсказанию маска, по каждому пикселю. Примерами таких методов могут послужить мера сходства Жаккара, коэффициент Сёренсена, функции ошибки бинарная кросс-энтропия и метод наименьших квадратов и др.

         В результате определения ошибки, допускаемой данной архитектурой в процессе сегментации изображения, применяется метод обратного распространения ошибки, благодаря которому происходит корректировка весов ядер свертки с последнего до первого, где последним определяют сверточный слой перед определением ошибки допускаемой данной архитектурой в процессе сегментации изображения.

РЕАЛИЗАЦИЯ МОДЕЛИ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ АРХИТЕКТУРЫ U-NET КЛАССА СВЕРТОЧНЫХ НЕЙРОННЫХ СЕТЕЙ

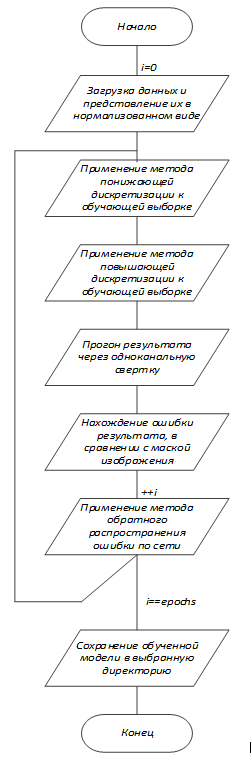
Алгоритм работы модели нейронной сети на основе архитектуры U-net класса сверточных нейронных сетей, применяемый с целью детектирования активных элементов на фотографиях печатных плат приведен на рис. 2.  Данный алгоритм отличается от классической архитектуры нейронной сети U-net класса сверточных нейронных сетей наличием в нем реализации приведения входного изображения к необходимому размеру, из-за существующих ограничений вычислительной мощности, выделяемой для решения поставленной задачи.

Для решения данной задачи были выбраны следущие параметры модели нейронной сети, построенной на основе архитетуры нейронной сети U-net:

- Размер обучающей выборки 150 изображений (выбран на основе ограниченной возможности создания масок изображений из обучающей выборки и компановки самого датасета, из-за ограниченности по времени); стандартные размеры обучающей выборки, которые не приведут к переобучению модели нейронной сети или другим не менее опасным ошибкам, возникающим при обучении, находятся в диапазоне 5000-15000 изображений, тут действует принцип – «Чем больше, тем лучше!», но не стоит забывать, что для такой массивной обучающей выборки нужно подходящее оборудование для его обработки, которое включает в себя не только возможности Вашего CPU, но и GPU.

- Функция ошибки бинарная кросс-энтропия

- Оптимизатор Адам

- Сжатие изображений на входе до 512х512х3, где 512х512 – ширина и высота изображения, а 3 – число каналов в изображении

- Batch-size 5; batch-size определяет размер входного пакета изображений на каждой эпохе обучений; размер должен подбираться на основе размера обучающей выборки, так как batch-size в основе своей определяет не будет ли достигнуто переобучение Вашей модели нейронной сети (Пример: размер обучающей выборки 100, batch-size 90 -> можно сделать вывод, что на каждой эпохе обучения будут повторяющиеся изображения, что приведет к «заучиванию» входного потока изображений -> переобучение модели нейронной сети)

- Количество эпох 500; как правило количество эпох определяется автоматически в зависимости качества проведения обучения, за счет наличия callback.

- Число каналов на каждом этапе 3-64-128-256-512-512-256-128-64-3-1; объяснение аналогично обоснованию размера обучающей выборки.

         Обучающая выборка была составлена на основе скаченных из сети Интернет фотографий печатных плат. В связи с ограничением времени, выделенным на обработку изображений и составление из них обучающей выборки, размер обучающей выборки составил 150 изображений. Для каждого изображения была нарисована маска – (в случае нормализации – бинарное) одноканальное изображение, описывающее местоположение искомых объектов на изображении. Пример маски и соответствующего изображения приведен на рис. 3. Проводя обучение модели нейронной сети, был сделан вывод о недостаточном объеме обучающей выборки, в связи с чем модель, во время обучения, быстро достигает этапа переобучения. Оптимальный размер обучающей выборки 1000 – 1500 изображений, с учетом вычислительных ограничений.

         В роли функции ошибки была выбрана бинарная кросс-энтропия. Значение функции ошибки – бинарная кросс-энтропия вычисляется по формуле, приведенной на рис. 4. Данная функция ошибки выбрана на следующем основании – в связи с тем, что изображения, образующееся на выходе нейронной сети и маска, соответствующего на выходе изображения, представляют собой бинарные (так как в данной модели реализована нормализация обучающей выборки) одноканальные изображения. Исходя из этого, бинарная кросс-энтропия, как функция ошибки, подходит для решения данной задачи лучше всего.

         Оптимизатор – Адам. Для решения данной задачи были выдвинуты две идеи: использование оптимизатора RMSProp или градиентный спуск с импульсом Нестерова.

Использование оптимизатора RMSProp позволило бы сократить количество коррекций ядер свертки на распространенных признаках, тем самым сократив обучение нейронной сети. Однако, применение градиентного спуска с импульсом Нестерова тоже подходит для решения поставленной задачи, благодаря наличию коэффициента, который отображает значение предсказания изменения функции. В свою очередь, оптимизатор Адам совмещает в себе два вышеописанных оптимизатора, за счет чего был использован в данной работе.

ЭКСПЕРИМЕНТАЛЬНОЕ ОБОСНОВАНИЕ ПОЛЕЗНОСТИ ОБУЧЕННОЙ МОДЕЛИ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ АРХИТЕКТУРЫ НЕЙРОННОЙ СЕТИ U-NET ПУТЕМ АНАЛИЗА ЧИСЛОВЫХ ХАРАКТЕРИСТИК ДОПУЩЕННЫХ ОШИБОК ПРИ ДЕТЕКТИРОВАНИИ

         Немаловажным этапом эксперимента является техническое обоснование его полезности.

В связи с чем, были выделены следующие характеристики качества обученности, которые прямо характеризуют его полезность:  

- Процент ошибок 1-го и 2-го родов на 100 тестовых изображений

- Коэффициент валидационной ошибки во время обучения

- Коэффициент валидационной точности во время обучения

- Время обучения и число эпох обучения

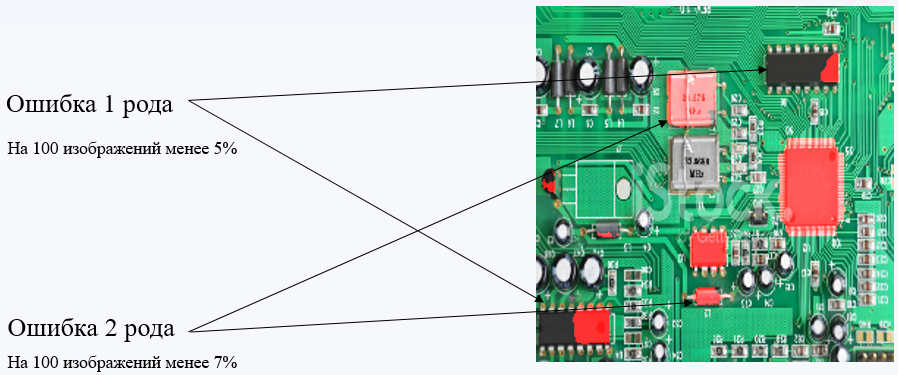
Ошибками первого и второго родов называются ошибки, допускаемые обученной моделью нейронной сети, проявляемые в распознавании объектов, не относящихся к искомым или в пропуске искомых объектов, в процессе сегментации изображений.

         Для подсчета процентного соотношения ошибочных результатов к общему числу результатов, необходимо за единицу измерения принять искомый объект. Тогда при расчете ошибок 1-го и 2-го родов подсчитаем общее число искомых объектов на 100-а изображениях. Для расчета ошибок первого рода необходимо подсчитать число всех найденных объектов, даже если найденный объект не относиться к классу искомых объектов. В случае расчета ошибки второго рода необходимо подсчитать число не найденных объектов, относящихся к классу искомых.

Для проведения статистического анализа качества обучения модели нейронной сети,

были обработаны 100 изображений с искомыми объектами. Результаты анализа следующие:

- Процент ошибок 1-го рода составил 5.5%

- Процент ошибок 2-го рода составил 6.3%

         Значением коэффициента валидационной ошибки будет являться значение ошибки обнаружения искомого объекта на сегментируемом изображении с применением валидации на последней эпохе обучения.

Значением коэффициента валидационной точности будет являться значение точности обнаружения искомого объекта на сегментируемом изображении с применением валидации на последней эпохе обучения.

Применение валидации при обучении модели нейронной сети является удостоверяющим фактором при определении ее обученности, так как валидация позволяет проверять модель на каждом этапе ее обучения, где этапом я называю каждую эпоху обучения, на качество ее обученности, путем сегментации изображений, не входящих в состав batch, т.е. мы будем получать данные о качестве обученности максимально объективные.

Говоря о времени обучения и количестве эпох потраченных на обучение, нельзя сказать, что эти два признака всегда являются объективными. Но в большинстве случаев, при обучении модели нейронной сети, представляющей собой модель, предъявляемые требования к которой обязуют получения от нее максимальной точности в обработке высококачественных изображений, время обучения и количество эпох будет достаточно большим.

НАПРАВЛЕНИЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ

         Дальнейшие исследования зависят от требований и задач, которые стоят перед данной моделью нейронной сети.

         Возможные направления дальнейших исследований:

- Повышение точности детектирования искомых объектов при сегментации изображений за счет увеличения обучающей выборки, увеличится разносторонность признаков детектирования.

- Внедрение многоклассовой классификации позволит под разными тегами детектировать объекты, относящиеся к разным классам объектов детектирования.

- Повышение точности детектирования искомых объектов при сегментации изображений за счет внедрения «плавающего окна», которое будет проходить по изображению высокого разрешения, подаваемого на вход модели нейронной сети и обрабатывать выделенные участки исходного изображения, за счет чего не будет потерь, которые возникали за счет сжатия изображений, в следствии чего возникали потери характеристик искомых объектов, благодаря которым обученная модель нейронной сети производит детектирование.

Ознакомиться со скриптом данной модели можете в GitHub:

https://github.com/IvIvanov2000/U-net/blob/main/U-net%20(Tranning-%D0%B2%D0%B5%D1%80%D1%81%D0%B8%D1%8F).txt