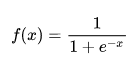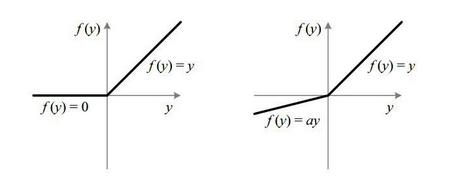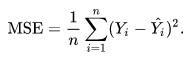Погружение в машинное обучение. Часть 1

Оглавление:

• Что такое искусственные нейронные сети?
• Виды обучения нейронных сетей
• Многослойные нейронные сети и их базовые понятия
• Разбираемся на примере
• Заключение

Что такое искусственные нейронные сети?

Данная статья предназначена для ознакомления читателя с искусственными нейронными сетями (далее ANN – Artificial Neural Network) и базовыми понятиями многослойных нейронных сетей.

Основным элементом ANN является нейрон. Его основной задачей является перемножение предыдущих значений нейронов или входных значений с соответствующими им весовыми коэффициентами связей между соответствующими нейронами, после активации вычисленного значения.

Основными задачами ANN является классификация, принятие решения, анализ данных, прогнозирование, оптимизация.

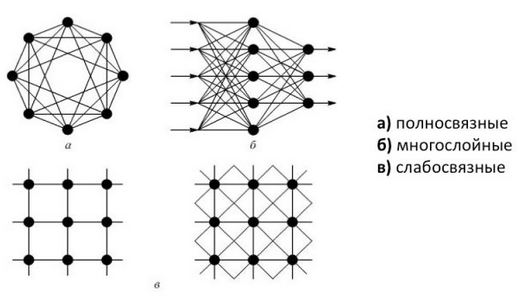
Искусственные нейронные сети категорируются по топологии (полносвязные, многослойные, слабосвязные), способу обучения (с учителем, без учителя, с подкреплением), модели нейронной сети (прямого распространения, рекррентные нейронные сети, сверточные нейронные сети, радиально-базисные функции), а также по типу связей (полносвязные, многослойные, слабосвязные). Такой значительно большой тип категорирования связан с разнообразием задач, которые ставятся перед ANN. Примеры, приведенные в скобках являются одними из самых распространенных типов категорирования, на самом деле их значительно больше.

Виды обучения нейронных сетей

Обучение с учителем

Данный тип обучения является самым простым, за счет того, что нет необходимости в написании алгоритмов самообучения. Для обучения с учителем требуется размеченный и структурированный набор данных для обучения. Под словом «размеченный» подразумевается процесс обозначения верного ответа на конкретный набор входных данных, который мы ожидаем от нейронной сети как результат работы. За счет таких данных нейронная сеть будет ориентироваться на разметку и корректировать процесс обучения за счет определения совершенных ошибок, которые будут определяться из данных разметки и ее предсказанных данных.

Обучение без учителя

Под обучением без учителя подразумевается процесс обучения нейронной сети без какого-либо контроля с нашей стороны. Весь процесс будет протекать за счет нахождения нейронной сетью корреляции в данных, извлечения полезных признаков и их анализа.

Существуют несколько способов обучения без учителя: обнаружение аномалий, ассоциации, автоэнкодеры и кластеризация.

На основе алгоритмов, описанных выше, в процессе обучения будет определяться значение ошибки, допущенной на каждом шаге обучения, за счет чего будет происходить корректировка обучения, следовательно, нейронная сеть обучится. За счет наличия алгоритмов, процесс написания которых занимает много времени и сильно усложняет моделирование нейронной сети, данный тип обучения считается самым сложным.

Обучение с подкреплением

Обучение с подкреплением или частичным вмешательством учителя можно считать золотой серединой в обучении нейронных сетей. Данный тип обучения представляет собой обучение без учителя с периодической его корректировкой. Корректировка обучения происходит тогда, когда нейронная сеть допускает ошибки при обучении.

Многослойные нейронные сети и их базовые понятия

Каждая ANN имеет входной, выходной и скрытые слои. Количество скрытых слоев и их сложность (количество искусственных нейронов) зачастую играют важную роль в процессе обучения, обеспечивая хорошее обучение модели нейронной сети.

Многослойными ANN называются нейронные сети, у которых количество скрытых слоев более одного. Пример многослойной нейронной сети:

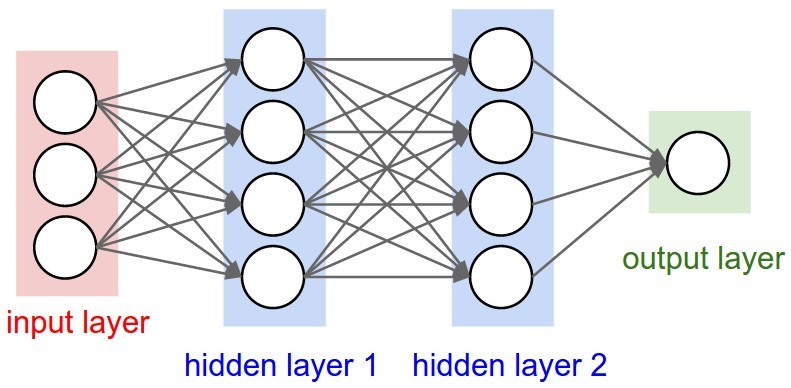
Входной, выходной и скрытые слои, нормализация и зачем все это нужно?

Входной слой дает возможность «скормить» данные, на которых требуется производить обучение. Выходной, в свою очередь, выдает результат работы нейронной сети. Вся суть заключается в скрытых слоях. Повторюсь, количество скрытых слоев и их сложность определяют качество обучения. Объясню на простом примере. Я, при написании модели нейронной сети, которая классифицирует рукописные цифры, смоделировал нейронную сеть из двух скрытых слоев по 30 нейронов в каждом. На вход подавал изображение 28х28 пикселей, но предварительно проведя нормализацию (объясню чуть ниже) входных значений и приведение изображения к виду 784х1, путем расставления всех столбцов в один. Т.е. входными значениями являлись 0 и 1, а если быть точнее - значения из данного диапазона. Так вот эти 0 и 1 оказались на входном слое, т.е. каждый нейрон входного слоя представлял из себя пиксель исходного изображения. Далее следовал скрытый слой, состоящий из 30 нейронов. Так вот, эти 30 нейронов представляют собой 30 участков исходного изображения, а каждый участок в свою очередь содержит какие-либо признаки, характеризующие изображение как определенную цифру. Т.е. чем больше нейронов в скрытых слоях, тем точнее будет представление и градуировка исходного изображения. Будет «плодиться» больше характеристик, по которым нейронная сеть будет классифицировать изображение должным образом.

Вернусь к такому понятию, как нормализация. Она необходима для приведения входных значений к значениям из диапазона 0 и 1. Смысл заключается в том, что нейронная сеть должна явно или с долей вероятности классифицировать изображение, или дать какое-то предсказание. Раз предсказание представляет собой вероятность, то и входные значения должны быть в диапазоне от 0 до 1. Поэтому нормализация, к примеру, значений пикселей изображения, происходит путем деления на 255, т.к. значения пикселей находятся в диапазоне от 0 до 255 и максимальным значением является значение 255.

Весовые коэффициенты

Каждая связь между искусственными нейронами обладает весовым коэффициентом, который постоянно изменяется в процессе обучения и является величиной, которая увеличивает или уменьшает предсказанную вероятность. К примеру, при уменьшении веса связи между 1 и 2 нейроном и увеличении веса между 1 и 3 получим, что, используя сигмоидальную функцию активации, значение на ее выходе в 1-ом случае будет стремиться к 0, а во втором к 1. Т.е. весовые коэффициенты являются своего рода возбудителями искусственных нейронов к прогнозированию.

Функция активация, виды и особенности

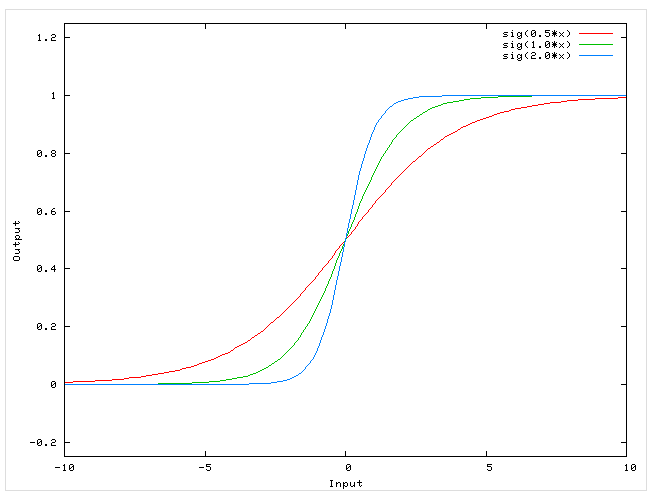
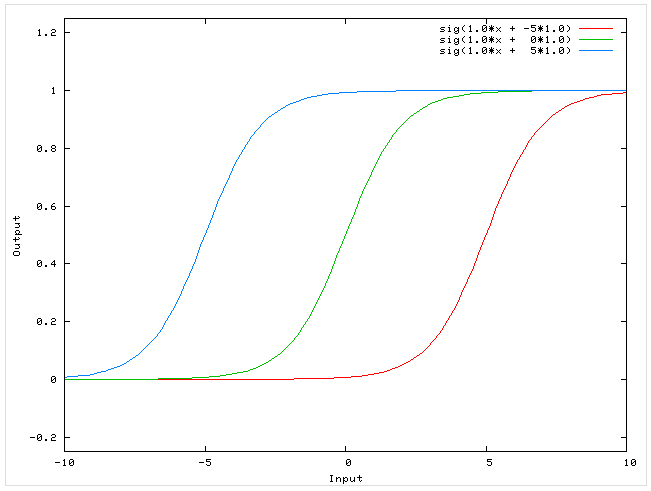
Функция активации является нормализующим звеном на каждом слое нейронной сети. Она представляет из себя функцию, которая приводит входное значение к значению от 0 до 1. Одной из самых распространенных функция активации является сигмоидальная функция активации:

Значение ‘х’ является значением, которое обрабатывается функцией активации. Оно включает в себя алгебраическую сумму произведений значений нейронов на предыдущем слое на соответствующие им связи с тем нейроном, на котором мы производим расчет функции активации, а также нейрон смещения.

Пример вычисления функции активации приведен на рис. 5

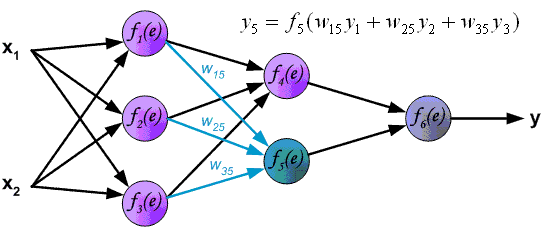
Распространенные виды функций активации:

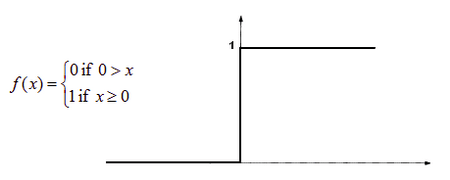
• Активация пороговой функции; функция активирована, если x, не активирована, если х<0

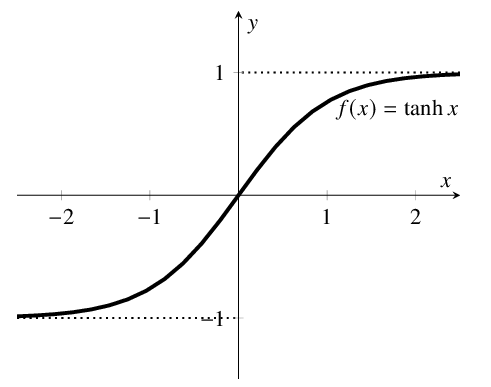
• Гиперболическая касательная функция ошибки; функция нелинейна, ее значения находятся в диапазоне (-1;1)

• ReLu и LeakyReLu; функция ReLu равна при х, при x, а при х<0 равна 0. Отличием LeakyReLu от ReLu является наличие коэффициента, определяющего значение функции при х<0 как ах

 Функция ошибки, виды

Функция ошибки необходима для определения ошибки прогнозирования, допускаемой нейронной сетью на каждом этапе обучения и корректировкой процесса обучения, за счет корректировки весовых значений связей между искусственными нейронами.

Примеры функций ошибок:

• Кросс-энтропия
• Квадратичная (среднеквадратичное отклонение)
• Расстояние Кульбака — Лейблера
• Экспоненциальная

 Самая простая и часто используемая функция ошибок (функция потерь) – среднеквадратичное отклонение.

Она вычисляется как половина от алгебраической суммы квадрата разности, прогнозируемого нейронной сетью значения и реальным значением – разметкой данных.

Backpropagation или обратное распространение ошибки

Для корректировки весов на каждом слое нейронной сети необходима метрика для определения ошибки каждого веса, с этой целью был разработан алгоритм обратного распространения ошибки. Он работает следующим образом:

• Вычисляется прогнозируемое нейронной сетью значение на выходе ANN
• Производится расчет функции ошибки, к примеру, среднеквадратичной
• Корректируются веса связей нейронов на последнем слое на основе вычисленной ошибки на выходе
• Происходит расчет ошибки на предпоследнем слое нейронной сети на основании скорректированных весов связей на последнем слое и ошибки на выходе ANN
• Процесс повторяется до первого слоя нейронной сети

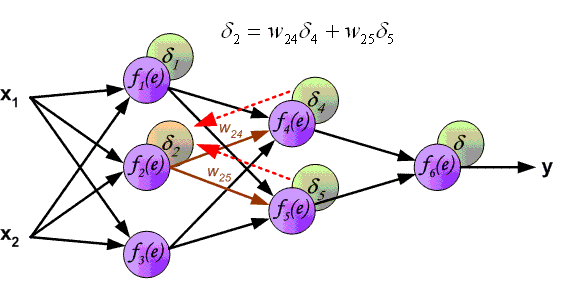
Пример работы алгоритма обратного распространения ошибки:

Bias или нейрон смещения

Значение смещения позволяет сместить функцию активации влево или вправо, что может иметь решающее значение для успешного обучения, а также позволяет быть более гибким при выборе решения или прогнозировании.

При наличии нейрона смещения, его значение тоже поступает на вход функции активации, складываясь с алгебраической суммой произведений нейронов и их весовых коэффициентов.

Пример работы нейрона смещения:

Разбираемся на примере

В данном примере напишем классификатор рукописных цифр на языке программирования С++. Обучающую выборку найдем на официальном сайте MNIST.

В первую очередь импортируем модули:

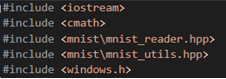
Определим обучающую выборку ‘dataset’, и загрузим в нее размеченные изображения MNIST.

Создадим входной слой равный 784 нейронам, так как наши изображения равны 28х28 пикселей и мы разложим их в цепочку пикселей 784х1, чтобы подать на вход нейронной сети; два скрытых слоя размера 30 нейронов каждый (размеры скрытых слоев подбирались случайно); выходной слой размером 10 нейронов, так как наша нейросеть будет классифицировать числа в диапазоне 0-9, где первый нейрон будет отвечать за классификацию числа 0, второй за число 1 и так далее до 9.

Необходимо сразу инициализировать наши значения слоев, к примеру 0.

Создадим матрицы весов между входным и 1-м скрытым слоями, 1-м скрытым и 2-м скрытым слоями, 2-м скрытым и выходным слоями, и инициализируем матрицы случайными значениями, как показано на рисунке. На примере значения весов находятся в диапазоне [-1;1].

Также необходимо создать массивы, которые будут содержать в себе значения алгебраической суммы произведения весов на соответствующие нейроны, как было описано выше в статье, после чего эти значения будут подаваться в функцию активации.

Ниже были созданы массивы ошибок на каждом слое. Для сохранения результатов ошибок на каждом нейроне, были инициализированы количество эпох и скорость обучения (определяет скорость перемещения по функции в поисках минимума во время обучения; необходимо быть осторожным с этим значением, так как если оно будет слишком мало, то, есть вероятность остаться в локальном минимуме, не найдя настоящий минимум функции или наоборот, при слишком большом значении, есть вероятность перескочить главный минимум функции.)

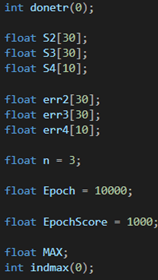
На данном этапе начинается процесс обучения нашей нейронной сети. Внешний цикл определяет количество эпох обучения, а внутренний количество итераций обучения в каждой эпохе.

На рисунке ниже инициализируются значения из обучающей выборки MNIST и занесения их на входной слой нейронной сети, а после происходит инициализация S-величин, о которых было сказано выше, нулями

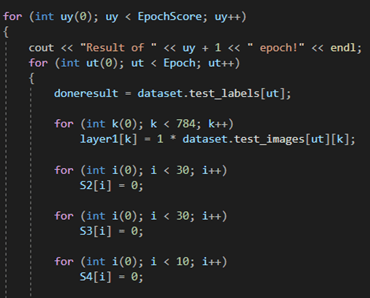
Ниже происходит подсчет алгебраической суммы значений произведений веса на соответствующий нейрон, а после прохождение их через функцию активации, где в роли функции активации выступает сигмоидальная функция.

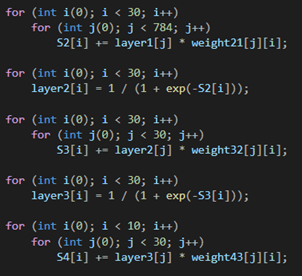
Подсчитав значения на каждом слое, происходит инициализация массивов ошибок, путем заполнения их 0, а также определение ошибок на выходном слое, путем вычитания полученных значений из 1, и последующим умножением на произведение значений нейронов прошедших через функцию активации на выходном слое на разницу между 1 и этими же значениями.

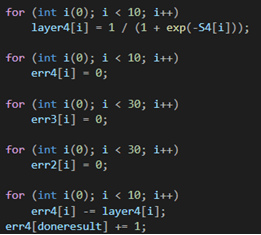
Далее необходимо определить ошибки на каждом слое нейронной сети методом обратного распространения ошибки. К примеру, чтобы найти ошибку на первом нейроне предыдущего слоя от выходного слоя, необходимо найти алгебраическую сумму произведения ошибок нейронов на выходном слое на соответствующие им веса связей с первым нейроном предыдущего слоя и перемножить на произведение значения нейронов на предпоследнем слое на разницу 1 и этих же значений. Таким образом необходимо найти допущенные ошибки нейронной сетью на каждом слое.

После определения ошибок, допущенных нейронной сетью на каждом нейроне, приступаем к корректировке весовых коэффициентов связей между каждым нейроном. Алгоритм корректировки представлен ниже.

Скорректировав веса, определяем максимальное полученное значение на выходном слое, тем самым определим ответ нейронной сети после прохождения через нее изображения.

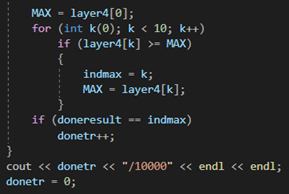
Заключение

В этой статье мы разобрались с базовыми понятиями искусственных нейронных сетей, а именно с такими как: входной, выходной, скрытые слои и их предназначение, весовыми коэффициентами связи между искусственными нейронами, функцией активации и ее предназначением, методами определения ошибки на каждом искусственном, с понятием нейрона смещения и функциями ошибки. В следующей статье мы перейдем к изучению нового класса нейронных сетей, таких как сверточные нейронные сети (CNN).

Желаю всем успехов в изучении!